|
HORIZONTE 3
|
|
|
||||
|
Archimedes von Syrakus (um 287-212 v. Chr., gr. Mathematiker, Physiker und Ingenieur) gilt als Entdecker des Hebelgesetzes. Ein Hebel ist eine Stange, die auf einen Dreh- oder Angelpunkt gesetzt wird. Durch eine solche Vorrichtung können auch schwere Lasten mit verhältnismäßig geringem Kraftaufwand in die Höhe gehoben werden. Um die Bedeutung seiner Entdeckung zu unterstreichen, formulierte Archimedes den Satz: „Gebt mir einen festen Punkt und ich werde die Erde bewegen“. Dieser fiktive Punkt, von dem aus sogar die Welt aus den Angeln gehoben werden könnte, wird seither als Archimedischer Punkt bezeichnet.
|
||||
|
||||
|
Der Archimedische Punkt hat Eingang in die Philosophie gefunden und steht dort für die Suche des Menschen nach einem absoluten (Bezugs-, Stand-) Punkt, von dem aus sich ein gesichertes Wissen über die Welt gewinnen lässt.
|
||||
|
Cogito ergo sum – Die Geschichte einer Trennung |
||||
|
Diesen Archimedischen Punkt der Gewissheit wollte auch René Descartes (1596-1650, fr. Philosoph, Mathematiker und Naturforscher) finden. In Meditationes de prima philosophia (2. Meditation, 1. Kapitel) schrieb er:
„Nichts als einen festen und unbeweglichen Punkt verlangte Archimedes, um die ganze Erde von ihrer Stelle zu bewegen, und so darf auch ich Großes hoffen, wenn ich nur das Geringste finde, das sicher und unerschütterlich ist." Descartes steht für den Versuch, die Philosophie und die Wissenschaft des Mittelalters neu zu begründen, waren sie doch stark vom dogmatischen Denken der Kirche beeinflusst. Als erstes beginnt Descartes damit, alles zu hinterfragen. An die Stelle der absoluten Gewissheit tritt vorerst der absolute Zweifel (2. Meditation, 2. Kapitel): "Ich nehme also an, alles, was ich wahrnehme, sei falsch; ich glaube, dass nichts von alledem jemals existiert habe, was mir mein trügerisches Gedächtnis vorführt. Ich habe überhaupt keine Sinne; Körper, Gestalt, Ausdehnung, Bewegung und Ort sind Chimären. Was soll da noch wahr sein? Vielleicht dies Eine, dass es nichts Gewisses gibt." Nachdem er so alles immer und immer wieder in Frage stellt und auch noch die hypothetische Existenz eines „genius malignus“ (böser Geist der Täuschung) annimmt, kommt er im 3. Kapitel der 2. Meditation zu folgendem Ergebnis: „Mag er mich nun täuschen, soviel er kann, so wird er doch nie bewirken können, dass ich nicht bin, solange ich denke, ich sei etwas. Nachdem ich so alles genug und übergenug erwogen habe, muss ich schließlich festhalten, dass der Satz "Ich bin, ich existiere", sooft ich ihn ausspreche oder im Geiste auffasse, notwenig wahr sei.“ In dieser Selbstgewissheit des Bewusstseins, im „Ich denke, also bin ich“ (ego cogito, ergo sum), findet Descartes schließlich seinen Archimedischen Punkt. Das denkende, kritische Ich wird ihm zum absoluten Fundament, zum ersten Axiom, von dem aus er Philosophie und Wissenschaft erneuern will. |
||||
|
||||
|
Descartes steht noch ganz in der Tradition der Substanzlehre der Antike und des Mittelalters. Darum setzt er das Ich, das cogito ergo sum, mit einer Substanz gleich, der res cogitans. Substanz ist für ihn: „Ein Ding, [...] das so existiert, dass es zu seiner Existenz keines anderen Dinges bedarf“. Das Ich ist von nun an außerhalb der Natur, soll es diese ja erst begründen.
Der Natur misstraut Descartes weiterhin. Allein in der Ausdehnung ihrer Objekte sieht er eine gewisse Realität und gesteht ihr deshalb eine eigene Substanz zu, die res extensa. Damit hat Descartes die Welt in zwei Substanzen, in die res cogitans und die res extensa geteilt. Da die eine Substanz die andere für ihre Existenz nicht braucht, wird es für Descartes schwierig zu erklären, worin denn nun die Wechselbeziehung zwischen Ich und Natur besteht, die z.B. in der Wahrnehmung eines Objektes durch ein Ich doch ziemlich eindeutig gegeben ist. Descartes ist sich der durch einen solchen Dualismus aufgeworfenen Probleme durchaus im Klaren. Er versucht, den entstandenen Abgrund zwischen Ich und Natur, Subjekt und Objekt, Bewusstsein und Materie, Innenwelt und Außenwelt mittels verschiedener Konzeptionen zu überbrücken: Im Allgemeinen ist es Gott, der als eine dritte Substanz (ungeschaffen und unendlich) zwischen den beiden von ihm geschaffenen, endlichen Substanzen durch göttliche Assistenz vermittelt. Im Besonderen ist es die Zirbeldrüse, die im Menschen eine Verbindung zwischen Bewusstsein und Körper herstellt. Diese beiden Konzeptionen sind für den Aufbau einer neuen Naturwissenschaft nicht sonderlich geeignet. Die eine ist zu abstrakt, die andere zu konkret und zudem wenig plausibel. Als wesentlich nützlicher hat sich hingegen etwas anderes erwiesen: das Kartesische Koordinatensystem. |
||||
|
Origo – Der Schatten des Ichs |
||||
|
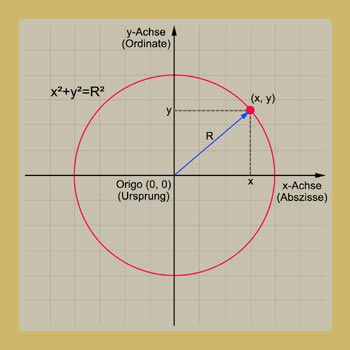
Je nachdem welche Methode zur Beantwortung geometrischer Fragestellungen verwendet wird, spricht man von Synthetischer oder Analytischer Geometrie. Die Synthetische Geometrie leitet ihre Sätze aus Axiomen und Postulaten her (wie in der Geometrie des Euklids) und verwendet dazu nur rein geometrische Argumentationen. In der Analytischen Geometrie hingegen wird durch Einführung eines Koordinatensystems jedem Punkt der Ebene bzw. des Raumes ein eindeutiges Zahlenpaar (x, y) bzw. ein Zahlentripel (x, y, z), die Koordinaten, zugeordnet. Dadurch eröffnet sich der Geometrie das Reich der Zahlen (Arithmetik) und abstrakten Gleichungen (Algebra).
Als Begründer der Analytischen Geometrie, die für die Entwicklung der Mathematik und der Naturwissenschaften der Neuzeit so ungeheuer erfolgreich war, gilt René Descartes. Seine grundlegenden Gedanken dazu hat er in dem Werk Discours de la méthode im dritten Anhang La géométrie niedergelegt. Das Koordinatensystem und die darauf aufbauende Analytische Geometrie sind keine (alleinige) Erfindung Descartes, aber er erkannte ihre Wichtigkeit für den Fortgang der Wissenschaften und sorgte durch seine philosophischen Schriften für die nötige Verbreitung. Von nun an ist das Koordinatensystem das verbindende Glied zwischen der zu erforschenden Natur, der res extensa, und dem denkenden Ich, der res cogitans. Die Natur wird in ein solches Koordinatennetz gleichsam eingefangen und durch Zahlen vermessen und mittels algebraischer Gleichungen beschrieben. |
||||
|
||||
|
Der Punkt (0, 0, 0), in dem sich die drei Achsen eines räumlichen Koordinatensystems schneiden, wird Koordinatenursprung oder Origo (lat. Herkunft, Ursprung) genannt. Wo das denkende Ich die Origo in der Natur platziert, ist frei wählbar. Darüber entscheidet allein die Zweckmäßigkeit. Im Geozentrischen Weltbild war es die Erde, im Heliozentrischen Weltbild die Sonne, und Immanuel Kant verlegte die Origo schließlich ins Ich, aber das ist eine andere Geschichte.
In dieser freien Wahl, das Koordinatensystem in der Natur an beliebiger Stelle positionieren zu können, liegt ein Rest Subjektivität. Die Physik hat darum ein eigenes Prinzip aufgestellt, welches fordert, dass physikalische Gesetze unter solchen Koordinatentransformationen kovariant (form-invariant) sein müssen. D.h. die Form eines physikalischen Gesetzes darf nicht davon abhängen, wie und wo das Koordinatensystem in der Natur liegt. Ersetzt man den Begriff Origo durch Beobachter, wie es die moderne Naturwissenschaft tut, dann kann die Forderung nach Kovarianz der Naturgesetze auch folgendermaßen formuliert werden: Die Naturgesetze müssen für einen Beobachter an jedem Ort des Universums und zu allen Zeiten die gleichen sein (Homogenität). Zudem dürfen sie nicht von der Beobachtungsrichtung abhängen (Isotropie) und davon, mit welcher (gleichförmigen) Geschwindigkeit sich ein Beobachter bewegt. Zusammengefasst wird eine solche Unabhängigkeit der Naturgesetze gegenüber einem Beobachter im Newton-Raum (bzgl. Ort, Zeit, Richtung und Geschwindigkeit) als Galilei-Invarianz bezeichnet. Das ist das Ideal und die Forderung einer jeden objektiven Naturwissenschaft: Die Natur muss sich vollkommen unabhängig von dem speziellen Standpunkt, den ein Beobachter in Raum und Zeit einnimmt, beschreiben lassen. Dieses Programm wurde so gründlich durchgeführt, dass die positivistische Wissenschaft schließlich die Existenz des absoluten Ichs - jenen Archimedischen Punkt, von dem aus Descartes die Naturwissenschaften erneuerte - vollkommen vergaß. Nur manchmal, wie in der Relativitätstheorie oder der Physik der Quanten, erschrickt man ein wenig, wenn sich der Schatten des denkenden Ichs wieder zeigt. Dinge die vorher unzweifelhaft als objektiv und absolut galten, wie z.B. Raum und Zeit, bekommen dann plötzlich eine subjektive Färbung, werden zu relativen Größen. Aber dieses Erschrecken der Naturwissenschaften über die plötzlich hereinbrechende Subjektivität in ihren Theorien beruht auf einer ungenauen Sichtweise. Dazu folgendes Beispiel: Im Jahre 1887 sollte das Michelson-Morley-Experiment die Existenz eines hypothetischen Äthers nachweisen. Das misslang zwar, aber dafür stieß man auf die absolute Konstanz der Lichtgeschwindigkeit. Unabhängig davon, ob ein Beobachter sich auf einen Lichtstrahl zu- oder von ihm fortbewegte, zeigte sich immer die gleiche Geschwindigkeit. Nach der Newtonschen-Galileischen Physik, wonach sich Geschwindigkeiten addieren oder subtrahieren, durfte es so etwas nicht geben. Auf Grund theoretischer Arbeiten von Albert Einstein und Hermann Minkowski stellte sich schließlich heraus, dass der von Isaac Newton und Galileo Galilei begründete dreidimensionale physikalische Raum die Wirklichkeit nur bei kleinen Geschwindigkeiten (im Vergleich zur Lichtgeschwindigkeit) einigermaßen genau abbildet. Eine exakte Beschreibung für alle Geschwindigkeiten wird erst dann möglich, wenn der alte Raum durch ein vierdimensionales Raumzeit-Kontinuum ersetzt wird, den so genannten Minkowski-Raum. Auch wenn dieser der Anschauung kaum noch zugänglich ist, so ist er doch der die Welt exakter beschreibende Raum. Nun gehört zu jedem physikalischen Raum eine seine geometrische Struktur definierende Transformationsgruppe (im Sinne von Felix Kleins Erlanger Programm). Im alten Newton-Raum waren es die Galilei-Transformationen, im neuen sind es die Lorenz-Transformationen. Die in diesen Räumen formulierten Naturgesetze müssen form-invariant gegenüber der jeweiligen Transformationsgruppe sein, und nur die Größen einer Theorie sind objektive und absolute Größen, die unter solchen Transformationen invariant bleiben (d.h. vom Standpunkt eines Beobachters unabhängig sind). Kurz gesagt: Objektiv ist das, was für alle Beobachter gleich ist. Wird der Newton-Raum mittels der Galilei-Transformationen auf seine Invarianten untersucht, findet man solche wie Abstand im Raum, Zeitdauer, Masse etc., was gut mit unserer Vorstellung von objektiven Größen übereinstimmt. Im Minkowski-Raum aber, dem physikalisch exakteren Raum, sind die Zeitdauer und der (dreidimensionale) Raumabstand durch die Lorenz-Transformationen keine Invarianten, keine absoluten, sondern vom Bewegungszustand des Beobachters abhängige Größen. Dafür sind jetzt z.B. die Lichtgeschwindigkeit und die Eigenzeit (der vierdimensionale Abstand) beobachterunabhängige und damit absolute und objektive Größen. Das alles will besagen: Durch z.B. neue Daten aus Experimenten kann es geschehen, dass unser wissenschaftliches Weltbild einen Riss bekommt. Größen, die bisher als unumstößlich objektiv galten, sind es plötzlich nicht mehr. An ihre Stelle treten dann andere absolute Größen, und diese zwingen das Ich zur Konstruktion neuer und die Natur besser beschreibende Räume. Mit jeder Abstraktionsstufe, die das denkende Ich dabei zu höheren und abstrakteren Räumen ad infinitum hinaufsteigt, kommen neue, allgemeinere Invarianten ins Gesichtsfeld, werden vorher absolute Größen zu relativen Größen. Nur wenn das denkende Ich an den alten Räumen festhalten will, fällt ein Schatten von Subjektivität auf die Natur. Erst die Forderung nach Unabhängigkeit der Naturgesetze vom Ich, d.h. die Forderung nach Invarianz gegenüber einer bestimmten Gruppe von Transformationen (Beobachterperspektiven), generiert die objektiven Größen einer Theorie. Das Descartsche Ich ist unsichtbar und an einem imaginären Ort außerhalb der Natur, aber es zeigt sich in den objektiven Größen seiner die Welt beschreibenden physikalischen Theorien, die es konstruiert. Die von einem Koordinatensystem aufgespannte Raumzeit, zum Zwecke einer objektiven Beschreibung der Welt, ist gleich einem Spiegel, darin das denkende Ich in die Invarianten seiner Theorie auseinander bricht. Das die Welt erforschende Ich projiziert sich als symbolische Formen auf die res extensa – Landkarten, mit deren Hilfe es versucht die Geheimnisse der Natur zu ergründen. |
||||
|
||||
|
Da jedes Ich immer auch Mittelpunkt seiner Horizonte ist, soll in der Fortsetzung der Frage nachgegangen werden, zu welchem Ich eigentlich der unendlich ferne Horizont des Universums gehört.
|
||||
|
© Copyright Peter Liendl und Gisela Klötzer |
home - back - top